三.希腊值的含义
序:各种希腊值特性
delta
call 的价值变化:标的相对于行权价的变化
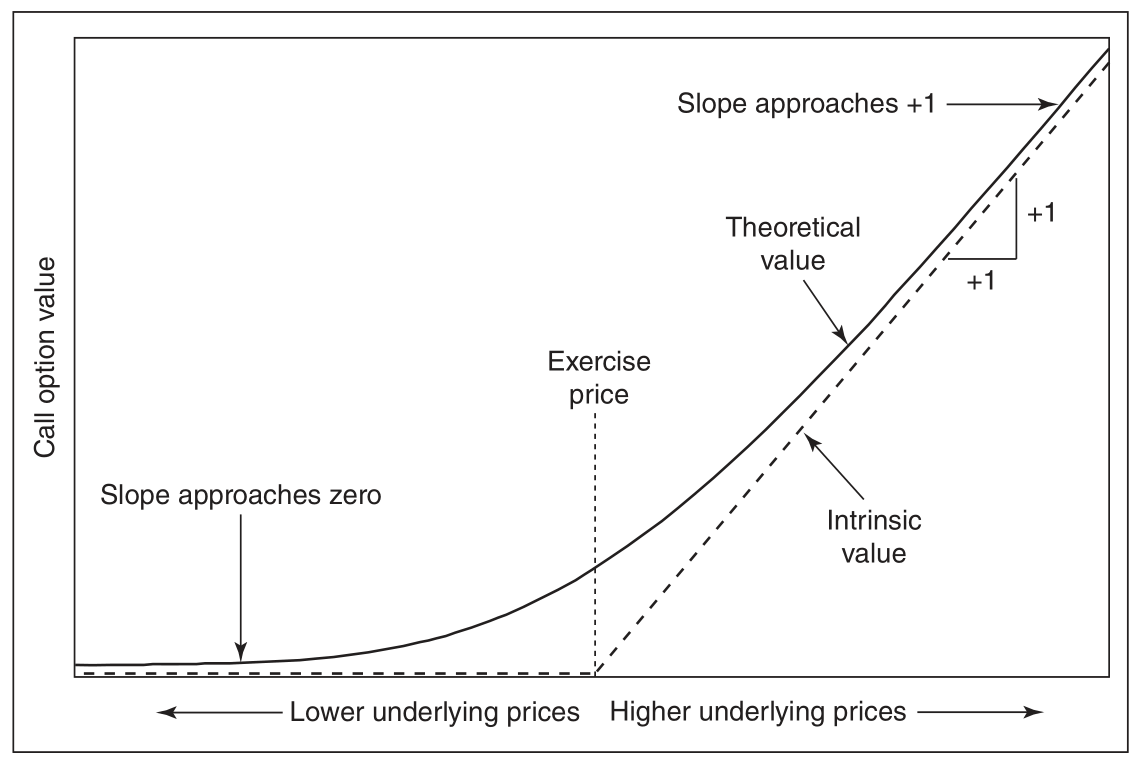
put 的价值变化:标的相对于行权价的变化
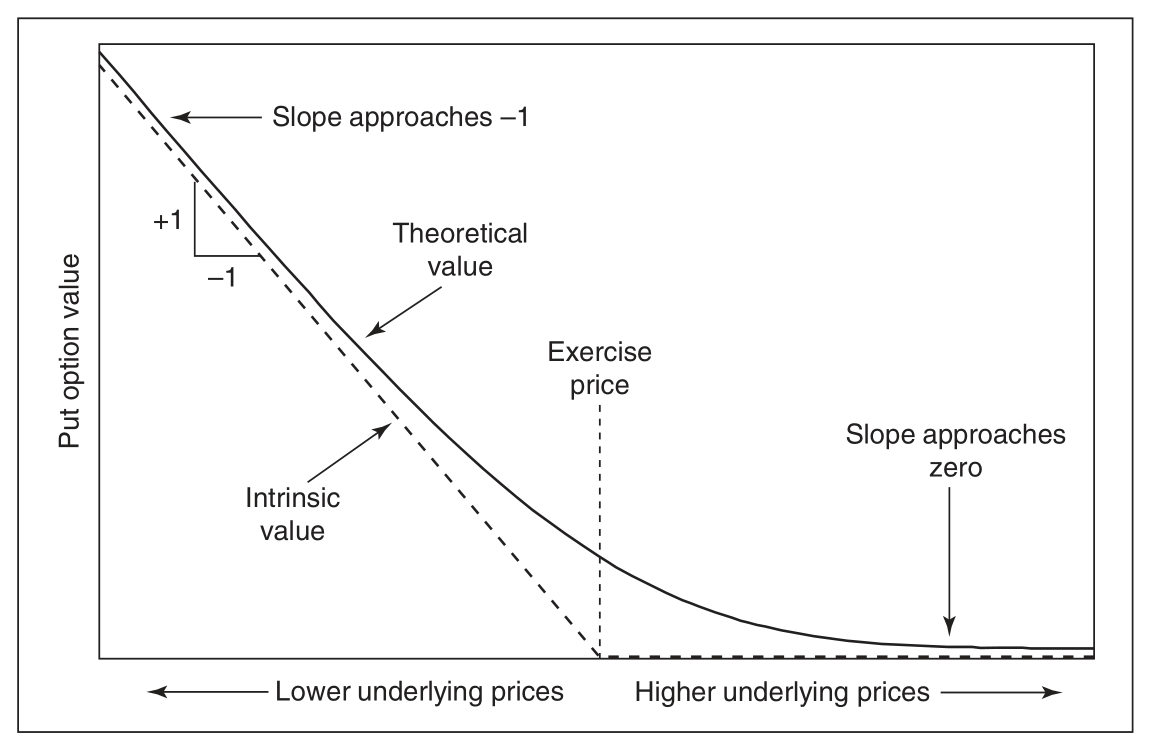
delta 随标的的变化
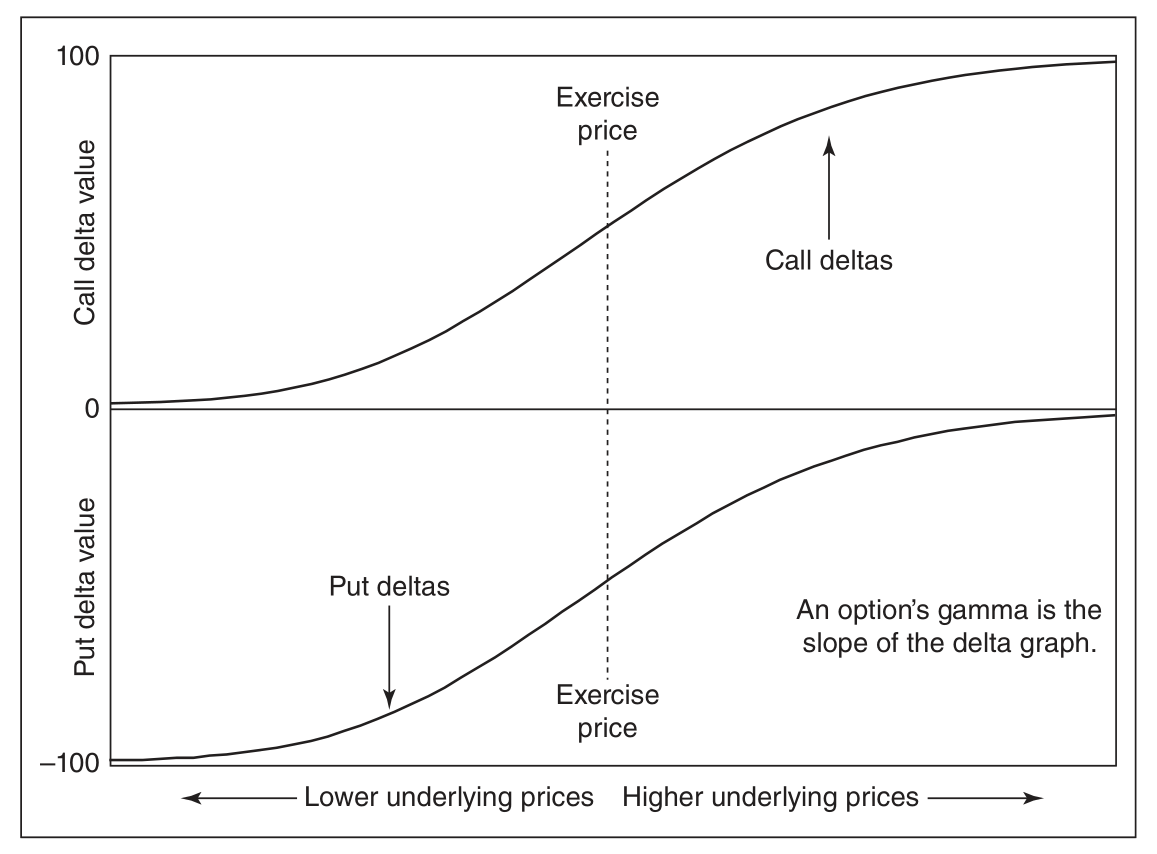
call_delta 随 volatility 的变化
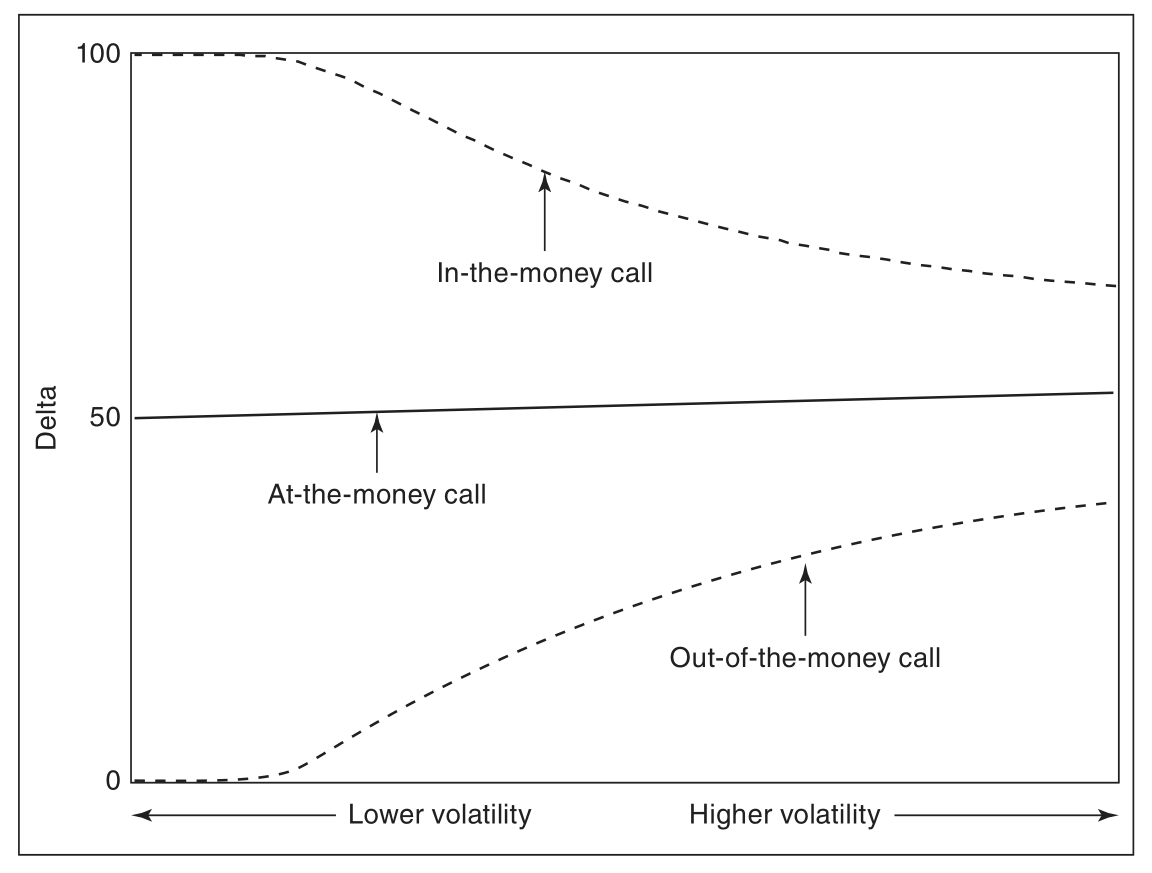
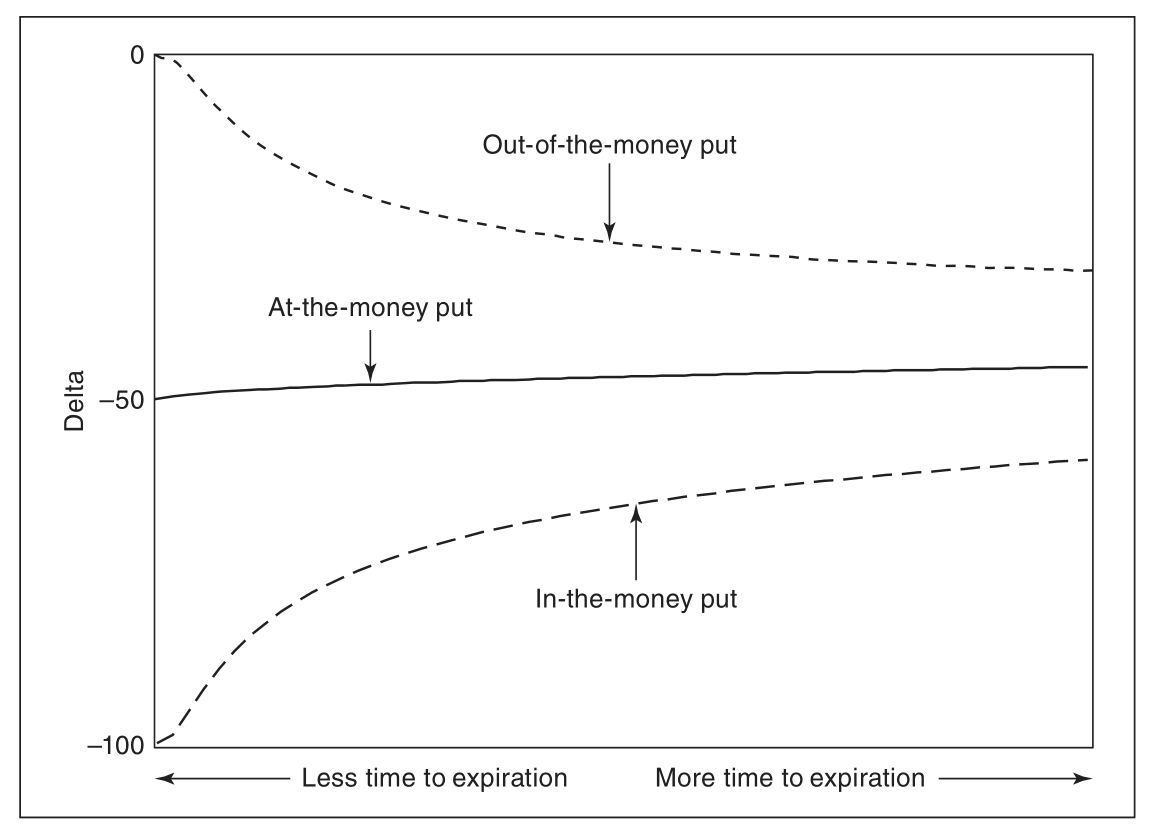
put_delta 随 volatility 的变化
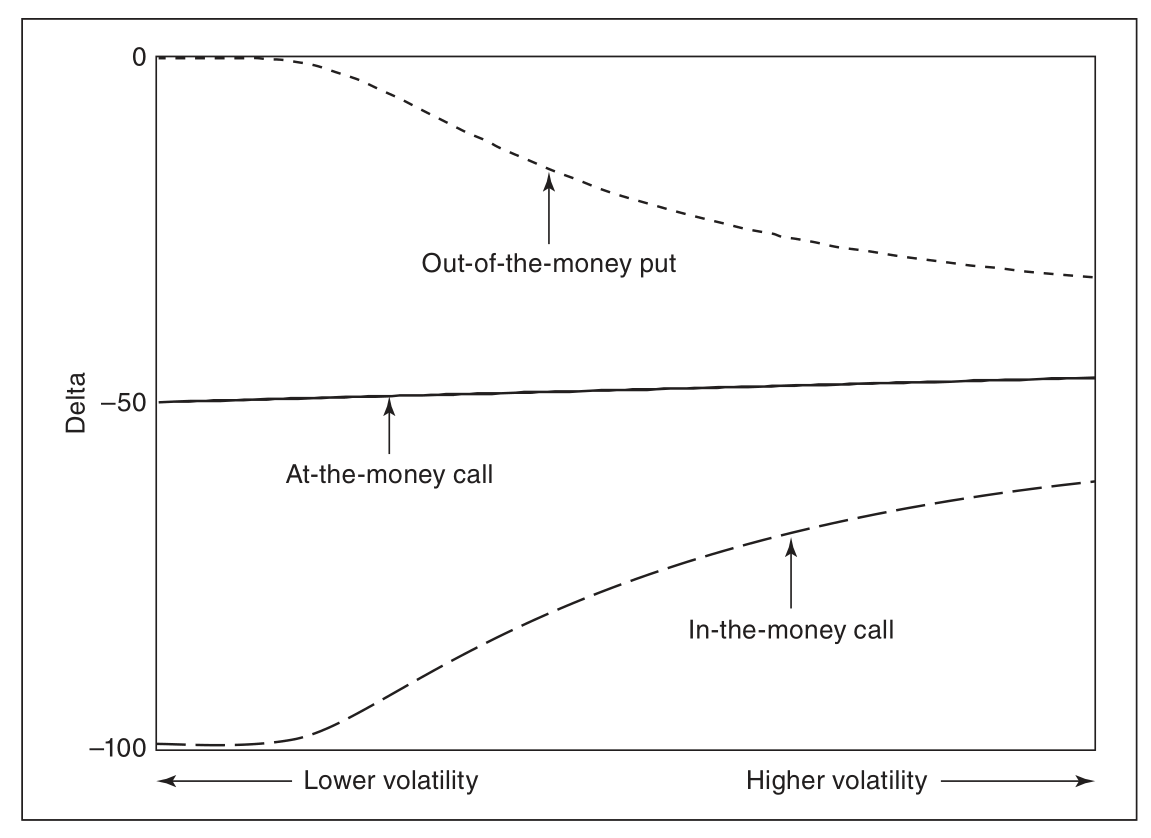
call_delta 随到期时间变化
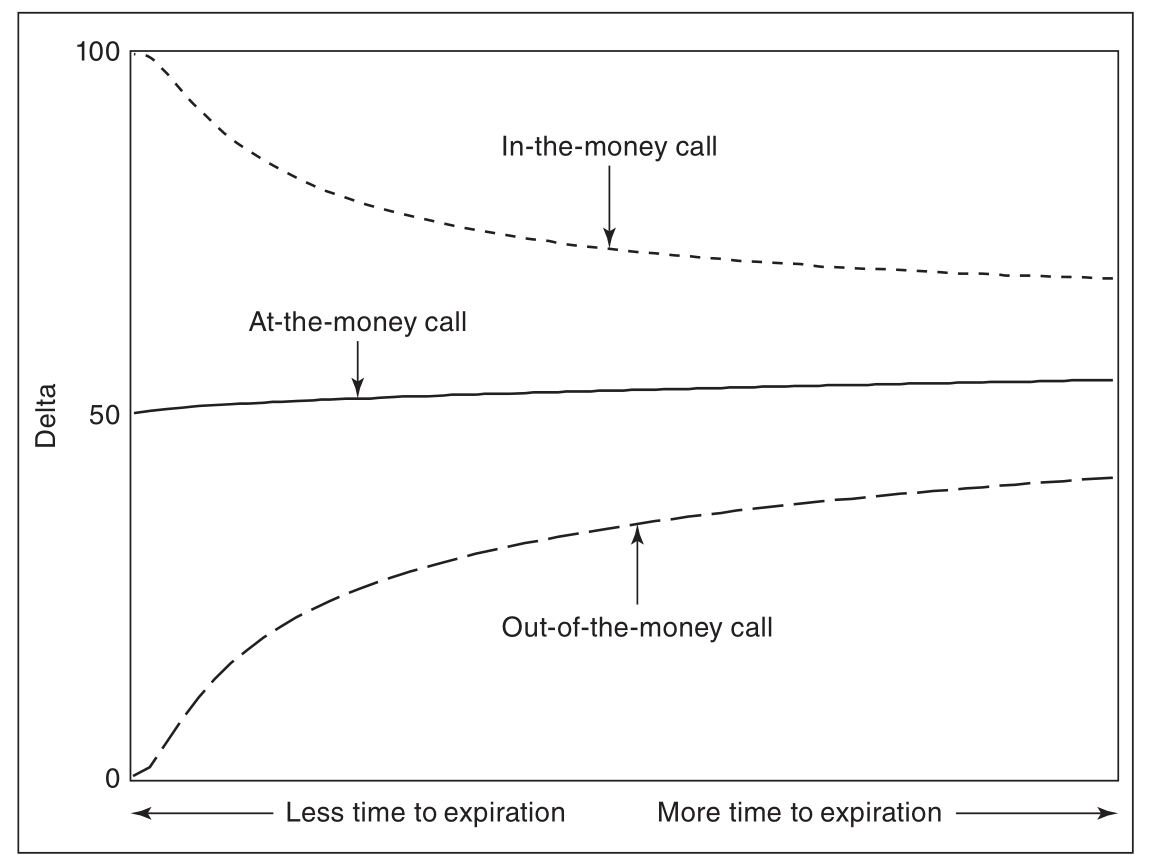
put_delta 随到期时间变化
call_delta 随着时间推移或者波动率下降的变化
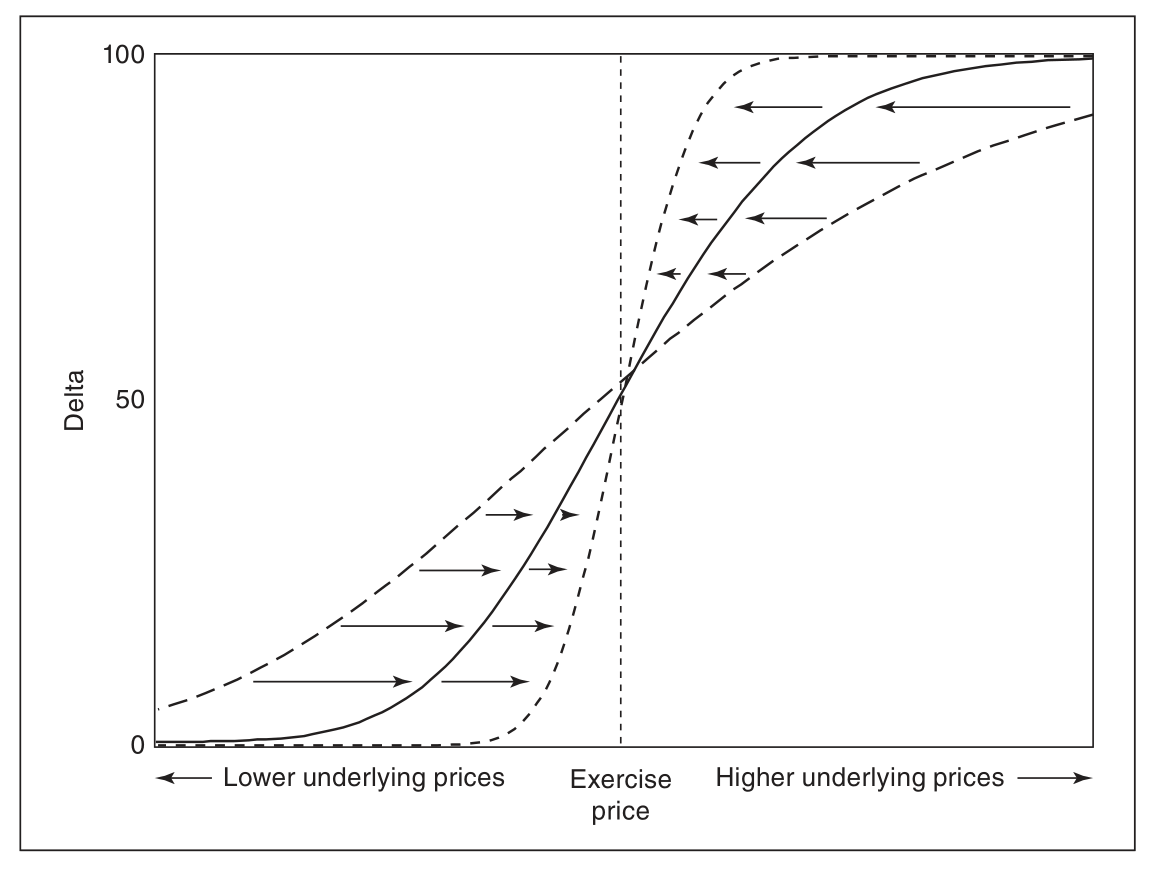
Vanna
Vanna:作为 Delta 对波动率的偏导,或者 Vega 对标的价格的偏导.
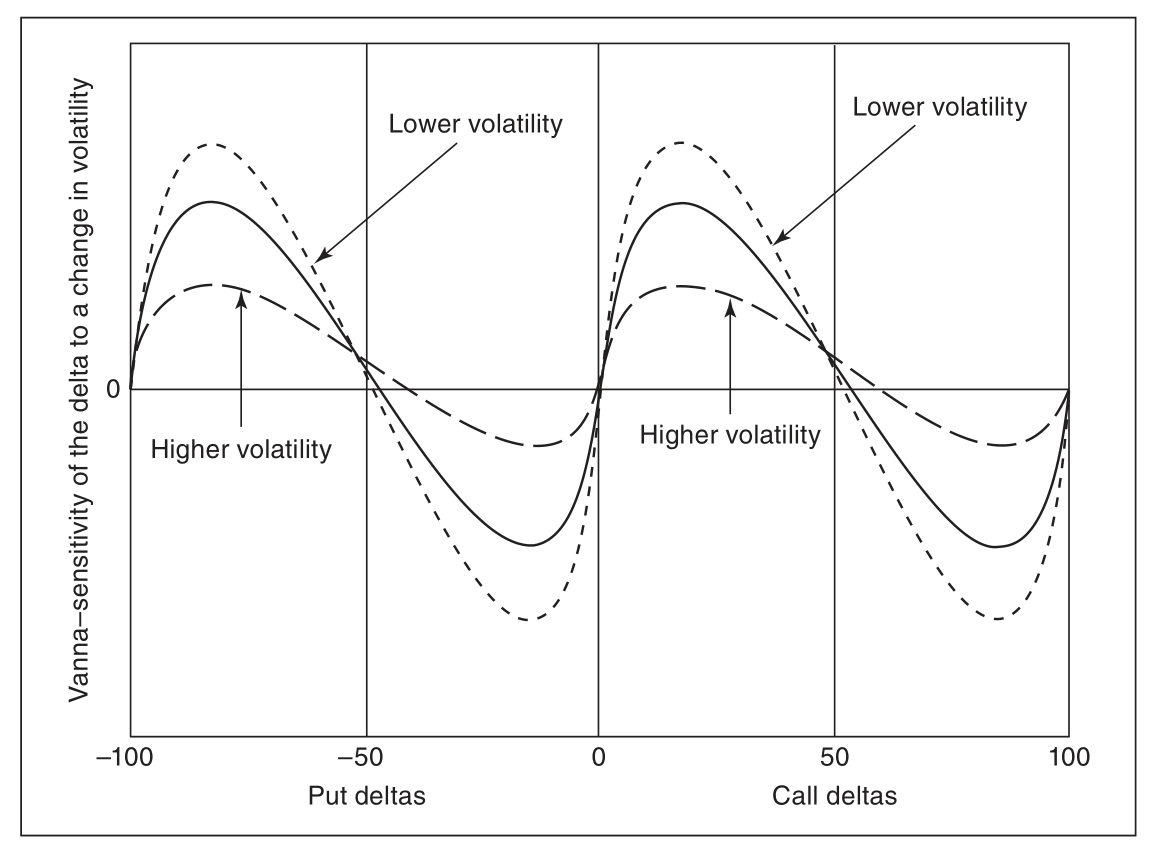
theta
theta:期权价格随着标的价格变化,此处取了绝对值(call 与 put 一样,都是负的!跟恒正 GAMMA 比较)
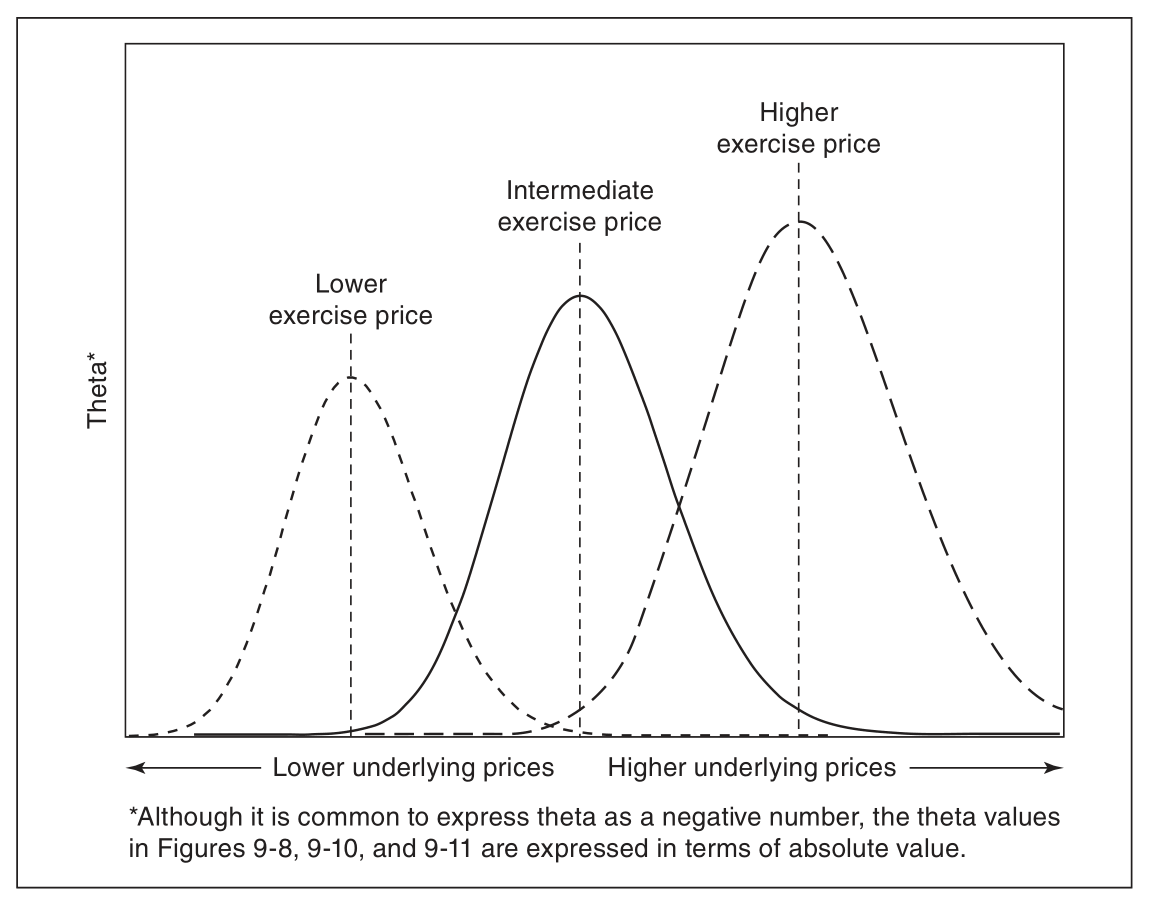
vega
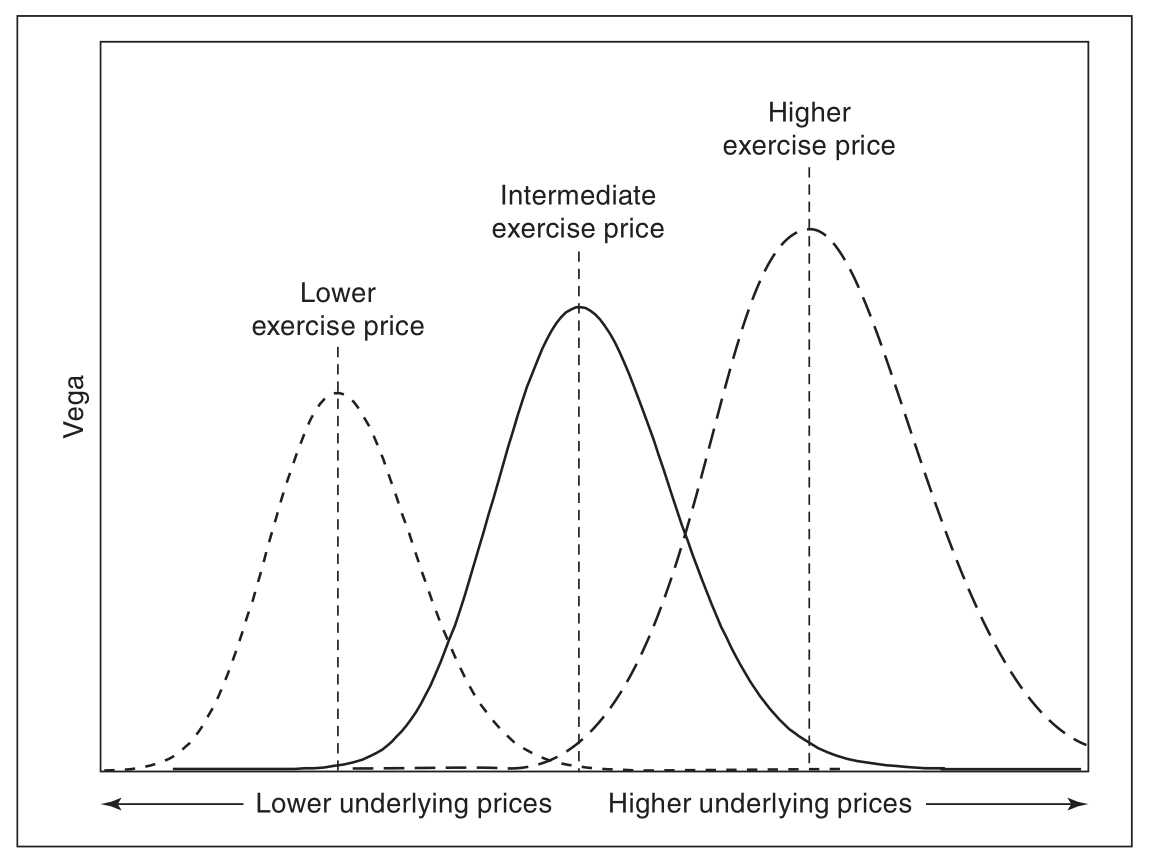
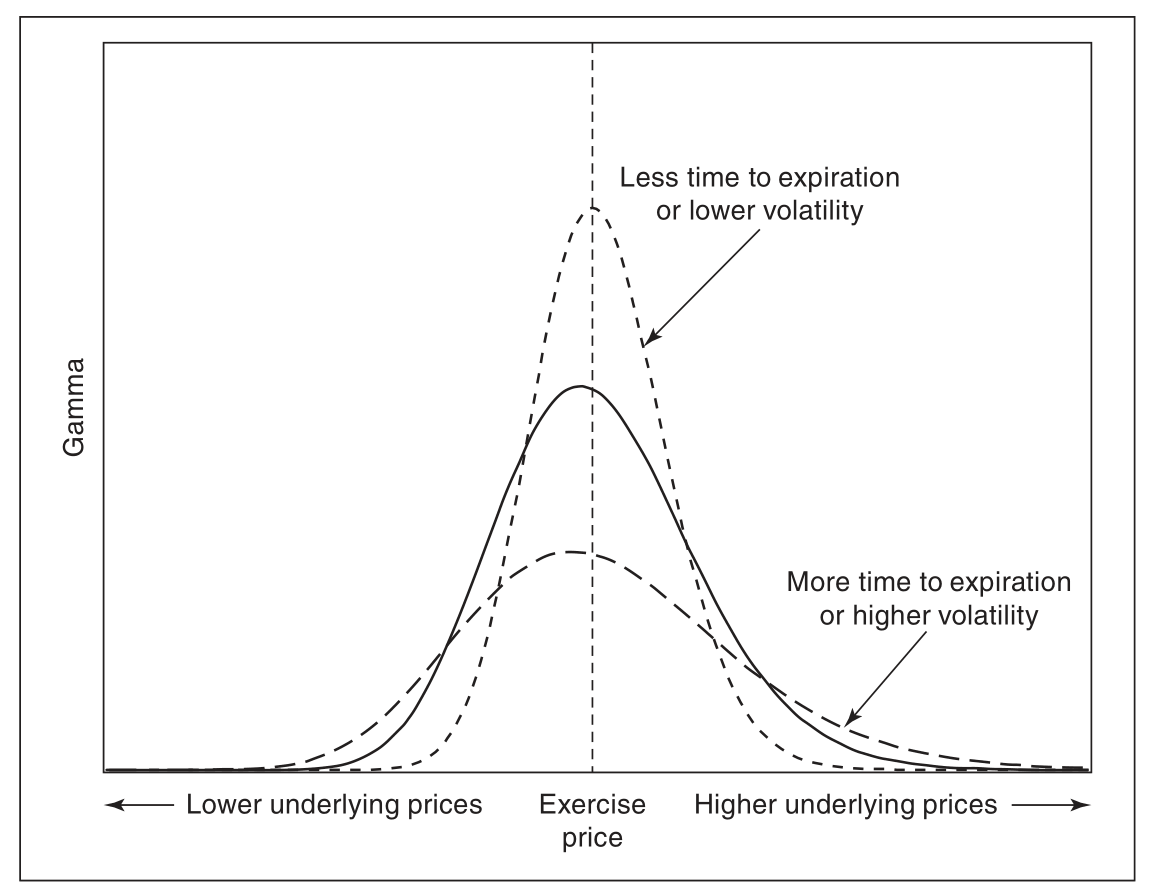
gamma
恒正的 GAMMA:
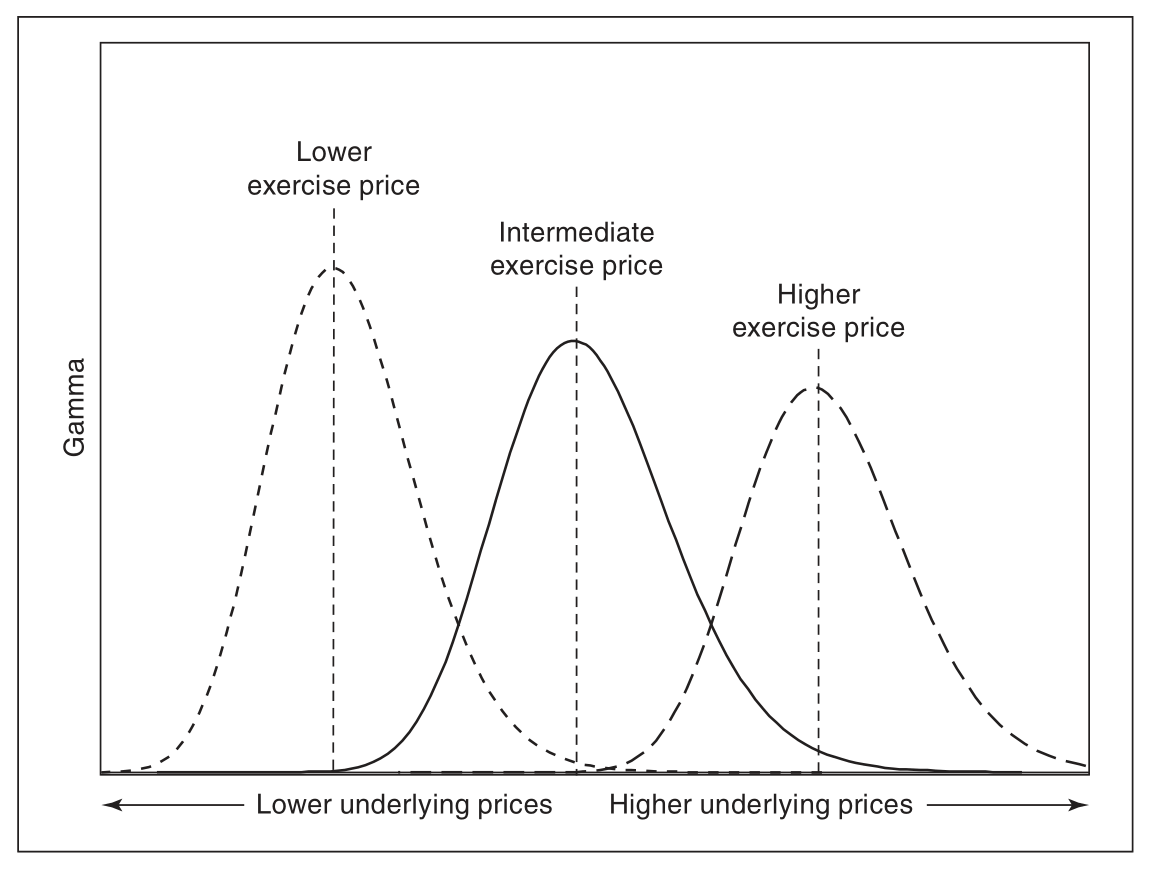
其中
3.0 随机分析几大基础定理
3.0.1 Radon–Nikodym
3.0.1.1 Radon-Nikodym 定理
测度空间 上定义有两个 -有限测度: 和 .定理表明:如果 (i.e. 关于 绝对连续),则存在一个 -可测函数 s.t. 可测集,
-有限: 是一个测度空间, 是上面一测度. 称为其上一个 -有限测度若 可以写成至多可列个有限测度集合的无交并.
绝对连续:实线上 Borel 子集上的测度 称为关于 Lebesgue 测度 绝对连续若对任何 的可测集 有 .记为 .
等价测度: 和 称为等价测度若 且 .
3.0.1.2 Radon-Nikodym 导数
上述函数 在几乎处处意义下唯一,通常写为 ,通常称为 Radon-Nikodym 导数.
3.0.2 Girsanov 定理
二次变差(quadratic variation):,,计算公式为 .
是 Wiener 概率空间 上的 Wiener 过程.令 是适应于 Wiener 过程生成的自然域流 的可测过程,.
定义 关于 的 Doléans-Dade exponential 如下: 其中 是 的二次变差.若 是严格正的鞅,那么可以定义 上的概率测度 s.t. 有 Radon-Nikodym 导数: 则对每个 , 限制在未扩充的 -域 上和 限制在 是等价的.进一步,若 是 下的局部鞅,那么过程 是 下的在 上的局部鞅.
推论:若 是连续过程, 是 下的布朗运动,那么: 是 下的布朗运动.
3.1 BS公式含义
Moneyness 指的是标的现价相对于行权价格的关系.下面考虑的是远期 F,
进行标准化后为:
下面我们记 ,故
标准的 moneyness 为如下均值: 大小关系为: 每级相差 ,这几项都在单位标准差内,所以把这几项转换成百分数,用标准正态的累计密度函数来评估.对这几个量的解释很精细(subtle),与风险中性测度有关.简单来说,有如下解释:
- 是二项 call option 的未来价值,或者风险中性下期权会在价内行权的可能性,with numéraire cash(风险中性资产)
- 是标准化的货币价值的百分比(概率?)
- 是 Delta,或者风险中性下期权会在价内行权的可能性,with numéraire asset(注意与上面的不同之处,cash 与 asset,债券与标的资产)
These have the same ordering, asis monotonic (since it is a CDF): 因为 是单调的(是一个CDF),他们有大小关系
3.2 计价单位的变换
wiki 概述:
在证券交易的金融市场中,计价单位的变换可以用来对资产定价.例如,若 exp 是 时刻投资在货币市场的 元在 时刻的价格,那么以货币市场定价的所有资产(记作 )在风险测度(记作 )下是鞅: 现在假定 是另一个严格正的交易资产(因此在货币市场的定价下是一个鞅),那么我们能根据 Radon-Nikodym 导数定义一个新的概率测度: 根据贝叶斯定理可以证明 关于新的计价单位 在 下是一个鞅:
知乎总结:
3.2.1 概述
在探讨计价单位变换之前,我们先来粗略的看一下这个公式长什么样子: ,这里 是一个计价单位 (Numéraire).乍一看,这个式子和风险中性定价公式 长得一模一样,只不过是将债券 替换为了另一个东西 ,然后从 测度下的期望变成了在 下的期望.
直观上来理解,就是这个意思,风险中性定价公式其实是以债券为计价单位,从而得出的资产的期望价值,那在某些情况下,我们也可以用其他资产作为计价单位,来对某些资产进行定价,或者是进行计算上的简化,这就是计价单位变换的动机所在.
其实可以看到,计价单位变换的本质,就是从一个 测度转化为另一个 测度,所以这个公式的核心,是找到连接两个测度的 Radon-Nikodym 导数 .
3.2.2 计价单位变换公式的推导
3.2.2.1 RN 导数的存在
这里我们想到的第一个问题是,对于任意一个给出的计价单位 ,存在这样的 RN 导数来定义测度 么?
这里我们需要注意的是,计价单位变换公式中,要求 是任意一个价格严格为正的资产,由先前的知识可以知道,这样的资产以债券计价时 (或者说以货币账户计价时) 是一个鞅,即 在测度 下是一个鞅,这样良好的性质,保证了 RN 导数 的存在性. >定理( 的存在性). 设测度 与 为 上的等价摡率测度,则存在 ,满足 ,且 .
根据这个定理,我们可以找到那个存在的 .可以验证,这样定义的 严格为正,且有 ,满足上述定理: 定义 RN 导数过程 ,可以证明 在原本的测度 下是一个 -鞅: (鞅性质).
3.2.2.2 RN 导数的性质
这里设 是由上一节中的定义 给出.
则在两个测度下期望的运算之间,可以用 RN 导数过程来联系.
设 为 -可测的随机变量.给定 ,则无条件期望之间的关系: 给出简单的证明: 更进一步的,给定 ,则条件期望之间的关系: 这里的其实是贝叶斯定理 (Abstract Bayes' Theorem) 的结论.
定理 (Abstract Bayes). 设 为 上的随机变量, 是 上由 导数 定义的测度.设 为 -代数且 ,则有: .
3.2.2.3 计价单位变换公式
首先我们有风险中性定价公式 ,接着根据定义的 RN 导数 ,可以得到:
对于 conditional on 的公式,根据 Abstract Bayes' Theorem 有:
3.2.2.4 新测度下的股价
根据这个计价单位变换公式,在实际运用时我们首先需要找到合适的计价单位 ,然后将风险中性定价公式中的 替换为 ,接着求一个在测度 下的期望 就可以了.
但要求出 ,我们还需要知道某个随机变量在 下的分布,或者说需要知道它新的 dynamics 是什么,此时还需要 Girsanov 定理来帮助我们找到 下的布朗运动 和 下的布朗运动之间的关系 .
定理 (Grisanov). 设 是 上的布朗运动, 为一个相适应的过程,定义指数鞅过程:,其中 是初值 的相适应的过程, 表示二次变差.则可以定义新的概率测度 .如果在概率测度 下 是一个布朗运动,那么: 在新的概率测度 下也是一个布朗运动.
我们这里以股价 为计价单位来运用 Girsanov 定理,找到 与 之间的关系.根据 的定义,有: 根据 Girsanov 定理,可以得到 ,于是在 下,对数价格 的 SDE 为:
3.2.3 一些栗子
根据风险中性公式, 0 时刻欧式看涨期权的价值应为: 此时,如果我们不想计算一个比较复杂的期望,则可以用 作为计价单位处理第一项,得到: 可以看到,我们其实是将原式转化为求事件 分别在 和 下的概率.
由上一节可以知道,在 下有 ,则:
此时可以很快的得到欧式看矤期权的定价公式:
上述推导也说明了, 表示在 下事件 的概率,即代表了在风险中性世界 中,该看涨期权在到期日被执行的概率,而 表示在 下事件 的概率,即 在以股价为计价单位的世界中,该看涨期权在到期日被执行的概率.